Die Lautstärke einer Schallquelle zu ermitteln, ist in der Praxis eine einfache Übung: Man wähle einen geeigneten Messpunkt, zücke seinen Pegelmesser und wenige Sekunden später wissen wir, wie viel Schall momentan auf unsere Ohren wirkt.
Doch wie sieht die Lautstärke fünf Meter vor oder hinter unserem Standpunkt aus, und was ist, wenn wir das ganze nur theoretisch planen und gar nicht vor Ort messen können? In diesen Fällen ist es gut, die wichtigsten Formeln in Bezug auf den Schallpegel und Distanzen zu kennen …
Schnellformel
Für eine Schallquelle mit kugelförmiger Abstrahlung im Freifeld gilt als theoretische Faustregel:

Beispiel
Eine Schallquelle besitzt in einem Meter Entfernung 78 dB SPL. Damit ergeben sich in zwei Meter Entfernung noch 72 dB (-6 dB) und in vier Meter Abstand 66 dB (-12 dB). Rücken wir hingegen um 50 cm Entfernung an die Schallquelle heran, steigt der Pegel um +6 dB auf 84 dB, in 25 cm Abstand erreicht die Messung 90 dB.

Genaue Berechnung
Hinter der einfachen Regel verbirgt sich die folgende Formel.:

Als bekannte Werte benötigen wir die beiden Entfernungen (D1 und D2) und den Pegel-/Bezugswert (SP1) am ersten Messpunkt.

SP1 = Schallpegel 1. Messpunkt, SP2 = Schallpegel 2. Messpunkt
Pegelrechner für Kugelstrahler
Verändere einen der drei Werte und berechne so den Schallpegel am zweiten Messpunkt sowie die Pegeldifferenz
Fehlende Distanz berechnen
Möchten wir hingegen die Distanz für den 2. Messpunkt ermitteln, hilft uns die folgende Formel weiter:
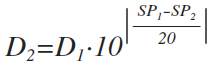
Beispiel Flugzeug
Ein startendes Flugzeug wird am Boden in 250 Metern Entfernung mit etwa 70 dB SPL gemessen. Welchen Geräuschpegel können wir in Flughöhe auf 2.500 Meter erwarten?
Eingetragen in den obigen Rechner oder die Formel für den Schall-Abstand erhalten wir bei 10-fachem Abstand eine Reduktion von 20 Dezibel und somit 50 dB SPL.

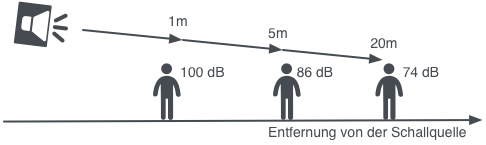
Beispiel Beschallung
Wir befinden uns 20 Meter vor der Bühne, das Messgerät zeigt einen Schallpegel von 74 dB. Da wir für eine weitere Messung in der ersten Reihe zu faul sind, berechnen wir den Schallpegel, der vermutlich knapp vor den Lautsprechern herrschen.
Faustformel
Mit der umgestellten Faustformel ergibt sich für den halben Abstand eine doppelte Lautstärke und somit: bei 20 m = 74 dB … bei 10 m +6 dB = 80 dB … bei 5 m +6 dB = 86 dB … bei 2,5 m +6dB = 92 dB bei 1,25 m +6dB = 98 dB … und mit etwas Kopfrechnen und Abschätzen bei 1 Meter Abstand 100 dB. Wer möchte, kann natürlich auch die Formel umstellen und erhält so ebenfalls 100 dB als Schalldruck.
Beispiel Stromgenerator
Ein Festival soll über einen Stromgenerator versorgt werden, dieser erzeugt laut Datenblatt in einem Meter Abstand 80 dBSPL. Welchen Abstand von Bühne und Publikum benötigen wir, um niemanden zu stören?
Wenn wir uns 30 dB Dämpfung, beziehungsweise maximal 50 dBSPL im Zuschauerbereich wünschen, muss der Generator mindestens 32 Meter entfernt stehen.

Zusammenfassung
Der Schallpegel nimmt, entgegen der Aussage mancher Webseiten, weder nach einer quadratischen Formel ab, noch können wir ohne Referenzwerte eine Aussage über „Dezibel pro Meter“ treffen.
Praktische Messungen vor Ort werden jedoch immer etwas andere Werte als in der Theorie ergeben. Abseits von „Laborbedingungen“ trägt die Absorption durch die Luft, das Verhalten unterschiedlicher Frequenzbereiche und in geschlossenen Räumen die Reflexionen ihren Teil zur Pegelerhöhung oder Dämpfung bei.