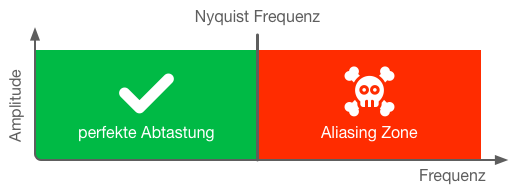
Jeder Verstoß gegen die Bedingungen des Abtasttheorems Fa > 2 Fn resultiert in einer fehlerhaften Abtastung, dem sogenannten Aliasing. Dabei werden alle Frequenzen über der Nyquist-Frequenz tiefer interpretiert als sie in Wahrheit sind. Selbst hohe Töne mit mehreren Gigahertz manifestieren sich als tiefe, vom Menschen hörbare Bassfrequenz.
Beispiele für Unterabtastung
Video
Animation
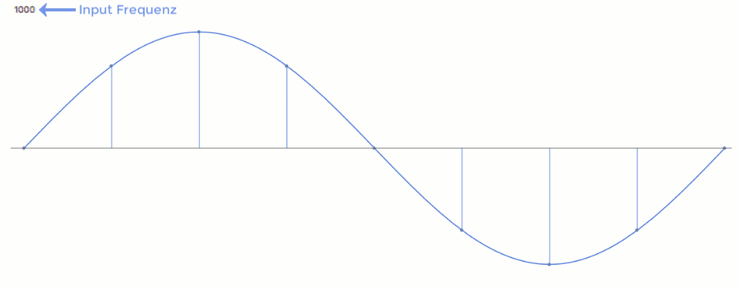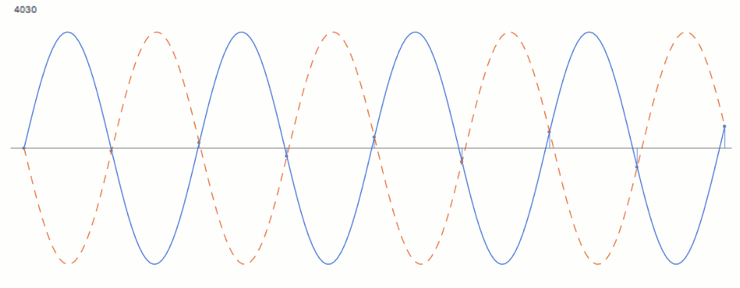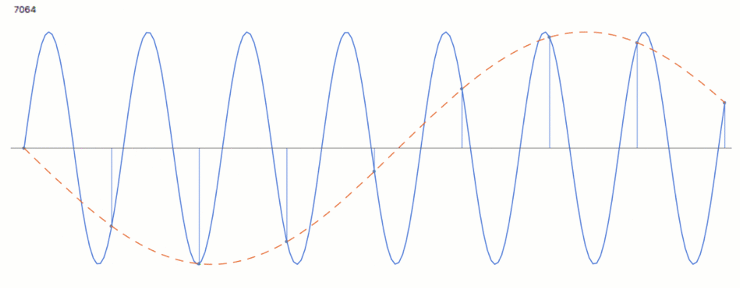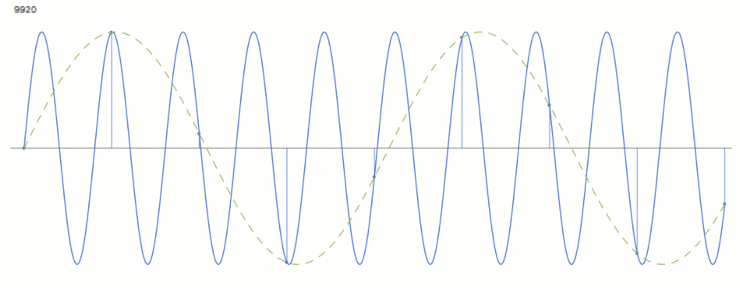
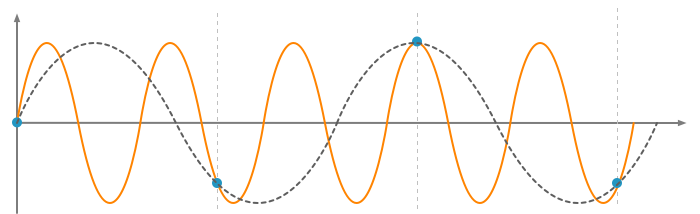
Fs < Fn
In den folgenden Beispielen variiert die eingehende Frequenz (orange) bei einem festem Abtastraster. Die blauen Punkte bilden die erfassten Werte, die grau-gestrichelte Wellenform ist die falsch-interpretierte Aliaising-Frequenz.
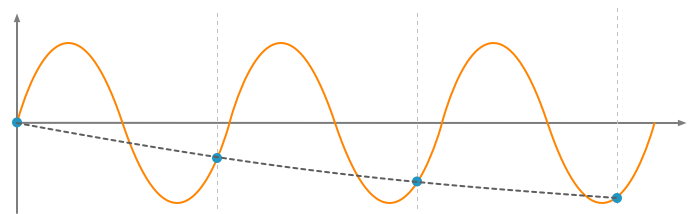
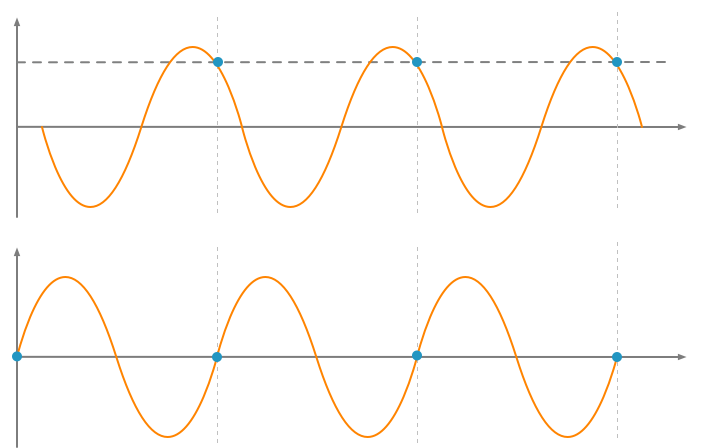
Fs = Fn
Stimmen Samplingfrequenz und Nutzsignal überein, entsteht eine Gleichspannung. Im unteren Beispiel liegen alle Erfassungpunkte exakt im Nulldurchgang.
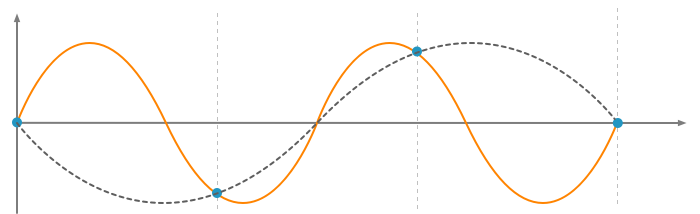
Fs = 2Fn
Auch bei der exakt doppelten Samplingfrequenz gegenüber der Nutzfrequenz ist noch eine Unterabtastung gegeben.
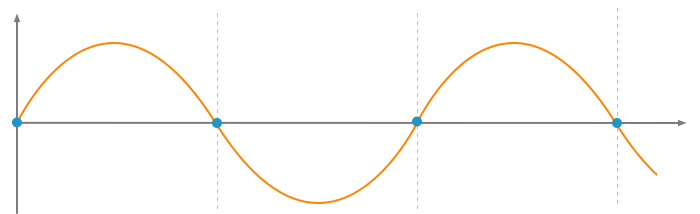
Einfach gesagt, befinden sich weniger als drei Abtastpunkte pro Periode, wird das Ergebnis verfälscht.
Wagon Wheel Effect
Die Auswirkungen des Aliasing sind nicht nur hörbar, sondern als „Wagon Wheel Effect“ auch sichtbar. In Abhängigkeit der optischer Abtastfrequenz (Bildern pro Sekunde) und der Rotationsgeschwindigkeit des gefilmten Objektes, erscheint sich dieses entweder nach vorne, nach hinten oder gar nicht zu bewegen. Bestes Beispiel hierfür sind Propeller oder Autoräder, beziehungsweise am Plattenspieler die Punkte des Drehtellers wenn die Stroboskopleuchte eingeschalten ist.